Що таке теорія ігор: приклади дилеми в’язня та особливості гри з нульовою сумою

Теорія ігор — один із найцікавіших інструментів сучасної науки, який дозволяє зрозуміти логіку людських рішень у ситуаціях конфлікту, співпраці чи конкуренції. Вона активно застосовується в економіці, міжнародних відносинах, бізнесі й навіть у штучному інтелекті. Найбільш відомими прикладами її практичного аналізу є дилема в’язня та гра з нульовою сумою, що демонструють фундаментальні принципи стратегічної поведінки, пише інформаційний портал Пушкінська.
Історія розвитку теорії ігор
Теорія ігор бере свій початок у роботах математика Джона фон Неймана, який у 1928 році опублікував дослідження про конкурентні ігри. Подальшого розвитку теорія набула у книзі «Теорія ігор і економічна поведінка» (1944), написаній фон Нейманом спільно з економістом Оскаром Морґенштерном.
У середині ХХ століття новий поштовх теорії дав Джон Неш, розробивши поняття «рівноваги Неша» — ситуації, коли жоден гравець не може покращити свій результат, не змінивши одночасно вибір інших. Ця ідея стала фундаментальною для аналізу переговорів, торгів і політичних стратегій.
Що таке теорія ігор простими словами
У центрі теорії ігор лежить припущення, що всі учасники діють раціонально, намагаючись отримати максимальну вигоду. При цьому кожен має враховувати, що його дії взаємопов’язані з діями інших.
Вона пояснює поведінку людей у ситуаціях:
- переговорів між країнами чи компаніями;
- економічної конкуренції на ринку;
- військових конфліктів і стратегій;
- колективних рішень у суспільстві.
Теорія ігор не гарантує точного результату, але допомагає передбачити ймовірні сценарії розвитку подій.
Дилема в’язня: чому вигода руйнує співпрацю
Дилема в’язня — класичний приклад, що демонструє протиріччя між особистим і колективним інтересом.
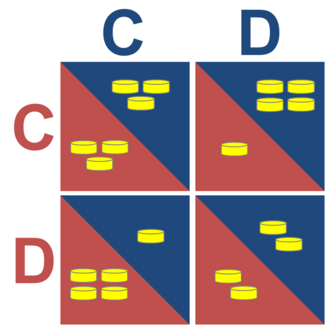
Проблема полягає в тому, що раціонально кожен обирає зраду, хоча найвигідніший для обох варіант — мовчати. Ситуація виглядає так:
- якщо обидва підозрювані мовчать — вони отримують мінімальний строк;
- якщо один зізнається, а інший ні — зрадник виходить на волю, а другий отримує максимальне покарання;
- якщо обоє зізнаються — вони отримують серйозне, але не максимальне покарання.
Це показує, як дефіцит довіри унеможливлює ефективну співпрацю навіть тоді, коли вона є логічно вигідною.
Гра з нульовою сумою: конкуренція без компромісів
Гра з нульовою сумою описує ситуації, де виграш одного завжди дорівнює втратам іншого. Загальний баланс завжди дорівнює нулю.
Класичними прикладами є шахи або покер, де результат одного гравця повністю протилежний результату іншого; валютні спекуляції, коли прибуток одних інвесторів = збитки інших та спортивні матчі з результатом «перемога–поразка». Варто зазначити: у реальному житті більшість конфліктів не є «нульовими», оскільки можливі взаємовигідні рішення. Але аналіз таких ігор дозволяє зрозуміти жорстку конкуренцію без можливості компромісу.
Рівновага Неша і практичне застосування
Одним із ключових понять теорії ігор є рівновага Неша. Вона виникає тоді, коли жоден гравець не може покращити свій результат, якщо інші не змінюють своїх рішень.
У бізнесі це пояснює цінові війни: компанії знижують ціни, доки не досягають рівня, коли подальше зниження шкодить усім. У політиці прикладом є стратегічні альянси, де учасники не ризикують змінити свою позицію, побоюючись втратити більше.
Сучасні приклади теорії ігор
Теорія ігор застосовується у багатьох сферах:
- економіка: аукціони, конкурентні ринки, торги;
- міжнародні відносини: переговори про роззброєння, кліматичні угоди;
- психологія: аналіз поведінки у групах, експерименти з довірою;
- технології: алгоритми в штучному інтелекті, автономні системи.
Завдяки універсальності підходу теорія ігор стала частиною міждисциплінарних досліджень і використовується навіть у медицині чи біології для моделювання поведінки популяцій.
Переваги та недоліки теорії ігор
Теорія ігор має значний вплив на сучасну науку та практику, але, як і будь-який підхід, вона не є універсальною.
Переваги
У сучасному світі, де рішення приймаються під впливом багатьох факторів, теорія ігор залишається інструментом, що поєднує науку, економіку й політику у спільному аналітичному полі.
- допомагає прогнозувати поведінку людей у складних ситуаціях;
- дозволяє моделювати сценарії від економіки до політики;
- формує основу для стратегічного мислення й переговорів;
- універсальна — застосовується в різних дисциплінах, від бізнесу до біології.
Попри обмеження, теорія ігор залишається одним із найефективніших інструментів аналізу стратегічних рішень.
Недоліки
Теорія ігор ґрунтується на припущенні, що всі гравці діють раціонально, що не завжди відповідає реальності; також вона не враховує емоцій, інтуїції чи культурних особливостей; а моделі часто спрощені й не відображають повної складності реальних подій.
Теорія ігор — це універсальна мова стратегічного мислення. Вона допомагає зрозуміти, чому у світі виникають конфлікти, як вибудовується співпраця й які сценарії найімовірніші у переговорах чи змаганнях. Дилема в’язня показує вразливість довіри, а гра з нульовою сумою — межі безкомпромісної конкуренції. Раніше ми писали про роль медіатора.